关于“移棋相间法”的新解释

作者姓名：孙设

单位机构：之江实验室

电子邮箱：sunshe@zhejianglab.org

一、  引言

1.“移棋相间法”及其历史背景

清顺治年间，中国的知识界便开始玩一种“移棋相间法”（又名“黑白相间法”）的游戏。移棋相间游戏，题目是这样的：

有N个黑棋子和N个白棋子，初始时黑棋子排在一边，白棋子排在另一边，且它们依次排列成一条直线。每次移动操作是：选择一对相邻的棋子，并保持它们的相对顺序，将它们交换位置。问：如何在N次操作内，使得棋子排列成黑白相间的顺序？

移棋相间游戏最早被记载于我国清代康熙年间成书的笔记小说《坚瓠集》 (成书于康熙年间，即1662年－1722年)中，书中记载“幼时见友人胡砺之将黑白棋子各三枚左右分列，三移则黑白相间．余因问曰:多亦可移乎，砺之曰:自三以至十外皆可移，多一子则多一移．余归试之，自三以至于十，果相间不乱．今已三十余年，偶雨窗复试，忘其大半，因绎数四始得就．”【褚人获：《坚瓠集》，戊集卷一，柏香书屋石印本。】

近代学者俞平伯祖父，清末俞曲园著《春在堂随笔》中有一段记载“长洲褚稼轩《坚瓠集》有移棋相间之法，……，余试之良然，而内子季兰复推广之，自十一子以至二十子” 。作诗记载此事，诗云：闲将棋子试推移，黑白分明亦一奇。此后空留遗法在，更谁灯下运灵棋。【俞樾：《春在堂随笔》，卷一，江苏人民出版社，1984年，第16页。】

日本著名数学史家平山谛著《东西数学物语》一书，叙述日本鸳鸯游戏和英国泰特问题时指出: “也许到日本明治时期后，由于日本和西方频繁的交通来往，这个游戏自然地从日本传到了西方，至今在中国文献中也没有发现类似游戏”．因此国际上误认为这一游戏起源于日本，事实上，最早的文献记载是中国，称为移棋相间。【平山谛. 东西数学物语[M]. 上海教育出版社, 2005.】

日本文献中最早的记载是1743年中根法舳著《勘者御伽双纸》一书中的“鸳鸯游戏”，抄录如下:

 “黑白棋子各有三个，如图所示，按黑白相隔放置

●(一) ○(二) ●(三) ○(四) ●(五) ○(六) ，

问如何移动一处的每两个棋子的位置使它变为如○○○●●●之形式?

法曰:使四五移至七八，一二移至四五，三四移至九十，则成为

一二三四五六七八九十

○○○●●●

图解这个过程如下:

一二三四五六七八九十

●○●○●○

●○●  ○○●

    ●●○○○●

        ○○○●●●

因为把黑白棋子来回移动操作，就如鸳鸯朝夕相处，悠然自得地在水面上游泳那样的缘故，所以，就产生了‘鸳鸯游戏’的名称．”【中根保之丞法舳. 勘者御伽双纸[J].】

明治12年（1879年），福田理轩的著作《算法玉手箱》中又给出了这个游戏的两个扩大形式，并给出了相应的解.【福田理轩. 和洋/普通算法玉手箱[J].】

林鹤一在明治32年（1899年）和大正14年（1925年），得到这个问题的一般解。【林鹤一博士和算研究集录》,昭和12年(1937年)刊,下卷第735页~747页.】

欧洲文献中最早的记载出现在1884年，当时英国物理学家泰特（Tait）在《哲学杂志》上发表了他的研究，研究中他将4枚金币（设为B）和4枚银币（设为A）按以下方式排列：

00ABABABAB

(1)BAABABA00B

(2)BAAB00AABB

(3)B00BAAAABB

(4)BBBBAAAA

欧洲把上述问题叫做泰特问题。【Tait. IV. Listingś topologie[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1884, 17(103): 30-46.】

1889年，法国数学家德拉诺伊（Henri Delannoy）在《自然》（La Nature）上给出了这个问题（镶符问题2色移2）的通解，即棋子移法通解公式，对所有正整数步的。他的这个通解和杨振宁给出的通解是完全一样的。【H. Delannoy, On Tait's Problem, La Nature (Science Progres Decouverte).】

在德拉诺伊以后还有不少人也独立的给出了这个同样的通解。数百年后的1920年代，我国数学家许宝騄（当时尚在读中学）和他的好友、"新红学"开拓者俞平伯，在阅读此书后，将上述规律推广至二十个棋子。许宝騄一年后总结出"合四为一"的新规律，据称一分钟即可讲解清楚，令听者豁然开朗。然而，由于后来的科研任务繁重，许先生未能将这一公式整理出来。俞平伯与许宝騄在中学时代便从清朝学者褚稼轩的著作中得知了数学游戏"移棋相间法"，并将其传播到西南联大的师生中。

1936年，交通大学教授姜长英在《交大季刊》上发表了一篇研究镶符问题（移棋问题）的文章。在这篇文章里，他给出了镶符问题2色移2的三个通解，其中的第一个通解和德拉诺伊的通解是相同的。【C. Y. Chiang（姜长英），移棋相间，交大季刊，第22期，1936.】

2019年，世界著名物理学家、诺贝尔物理学家杨振宁先生写了《许宝騄和“移棋相间法”》，完整记录下了他对该问题“Modulo4”解法的论证。【杨振宁. 许宝騄和 “移棋相间法”[J]. 数学文化, 2019 (4): 106-108.】

早在三十年代初，数学史家李俨（1892-1963）先生就对移棋相间问题产生了兴趣，他曾推测这一民间游戏与八卦或幻方有关，但没有述及上述史料【赵缭，李俨，黑白交错图，学艺，1932】。

2010年中国学者耿济证明发现移棋相间及其逆命题的移法都不是唯一性．同时应该指出移动过程中没有移动棋子的分布也不是唯一性．【耿济. 数学娱乐 (六)——移棋相间[J]. 海南大学学报: 自然科学版, 2010, 28(1): 1-10.】【耿济. 数学娱乐 (十六)——移棋相间问题与国际科研成果[J]. 海南大学学报: 自然科学版, 2015, 33(3): 197-203.】

从现代组合理论上来讲，移棋相间问题属于镶符理论的范畴，其实质是在某种特定的组合规则之下将一种序列重新组合成另外一种序列，例如将若干个以一维形式存贮于计算机内的数据按照类别重新分别存贮，又如用移位法来编制或破译密码，其原理都与移棋相间问题有某种相通之处【胡著信：“镶符问题的历史渊源和现代发展”，《中国数学史论文集》（二），山东教育出版社，1986年，第56-64页。】。

二、已有方案的新解释

解释：一个故事，

1.未来的岳母和未来的妻子说，女大当嫁。

2.岳父、岳母在一起商量，挑了个乘龙快婿。

3.母亲和我商定终身大事，相中了某个大小姐。

4.最终所有的有伴侣都成一对，情人终成眷属。

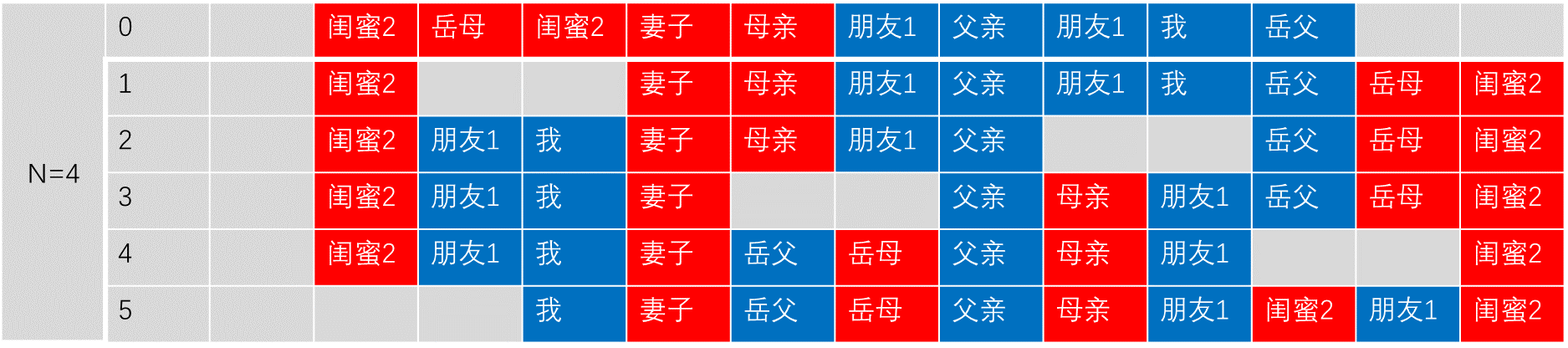
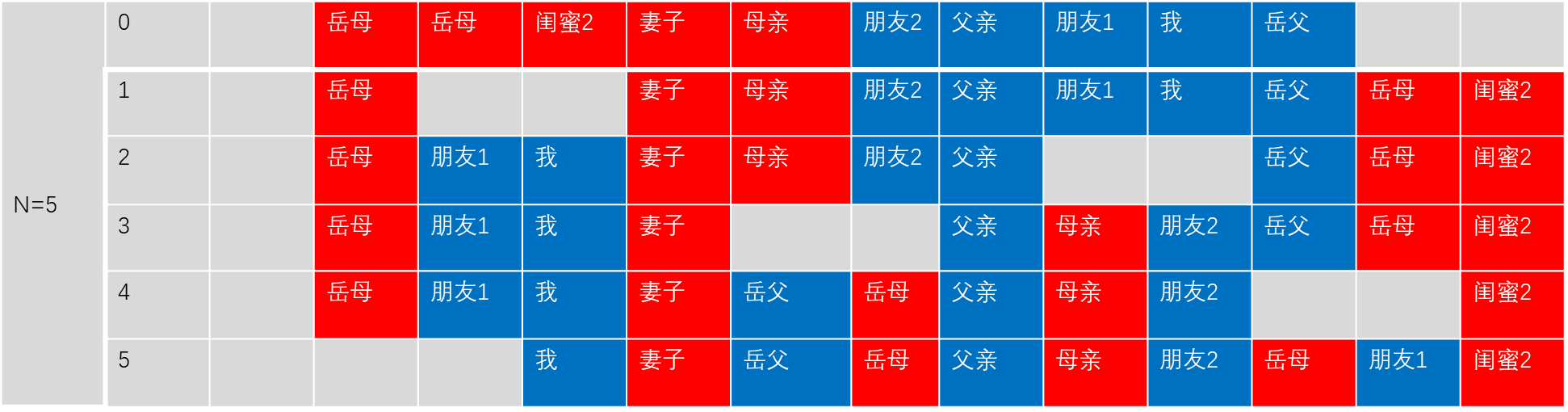
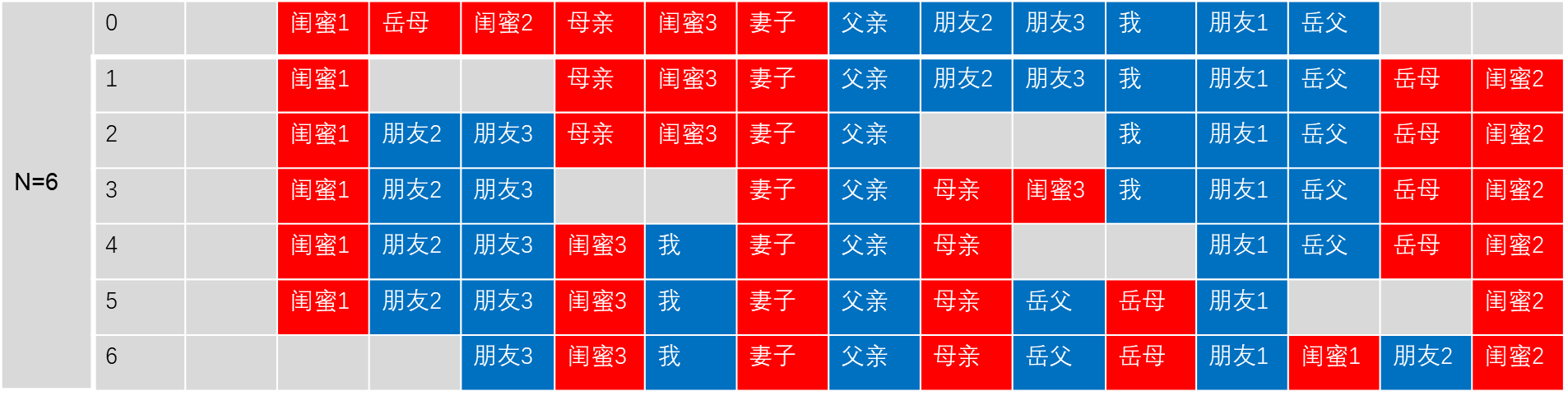
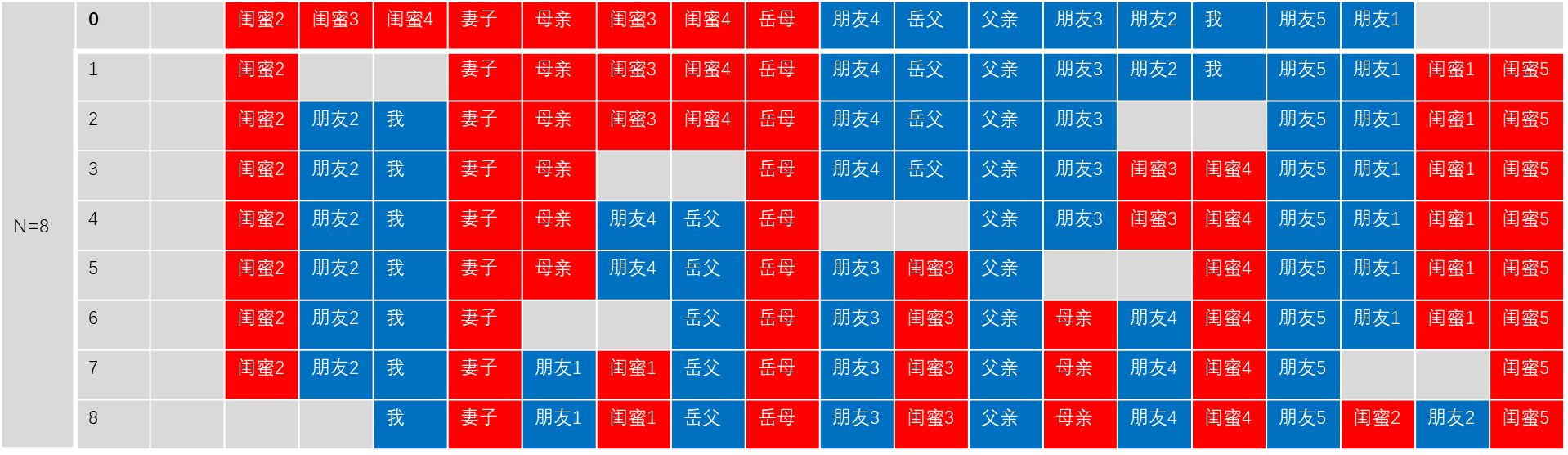
三、总结

从现实中的心理动力和行为模式来看，总是物理或心理距离较近的人先开始互动、沟通和移动。在“移棋相间”问题中，每一对“结婚”的伴侣，实际上对应着某种特定的解答。笔者在【Sun S, Ma S, Song J H, et al. Experiments and analyses of anonymization mechanisms for trajectory data publishing[J]. Journal of Computer Science and Technology, 2022, 37(5): 1026-1048.】的研究中指出，人类的轨迹具有高度的唯一性和可重识别性。在一定的分辨率和数据集规模下，90%的重识别概率可以用席慕蓉的诗《回眸》来解释：“前世的五百次回眸，换得今生的一次擦肩而过”。同样，重识别率未必达到100%，如王家卫电影《一代宗师》中的台词所说：“世间所有的相遇，都是久别重逢”。重识别率与分辨率的对数线性关系，可能可以通过排列组合的乘法原理来理解。从数学角度看，“移棋相间”游戏其实是一个关于缘分的隐喻，正如“十年修得同船渡，百年修得共枕眠”，而N值趋近于无穷，恰如我们不断推进的“移棋相间”游戏一样，永无止境。